Stanford offers this really cool free learning platform called Code in Place. I’m currently enrolled in the 2024 class and have finished my week 2.
There is this Optional problem called Checkerboard Karel, and this is my solution to it. I’m sure there are other ways to solve the problem, and feel free to let me know by commenting down below, or connect with me on Twitter/X.
The Problem
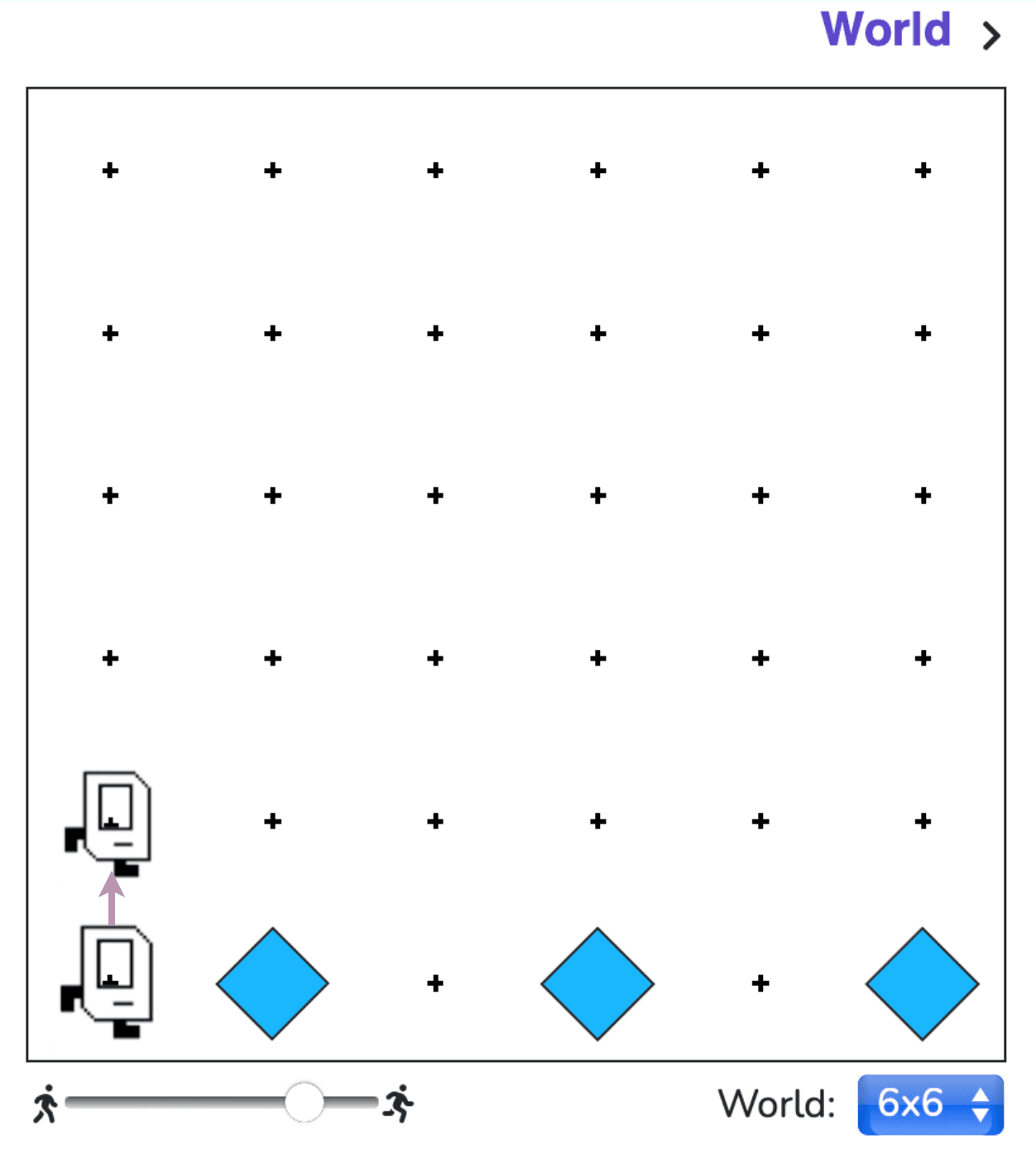
This problem asks us to get Karel to create a checkerboard pattern of beepers from an empty world to a world like this:
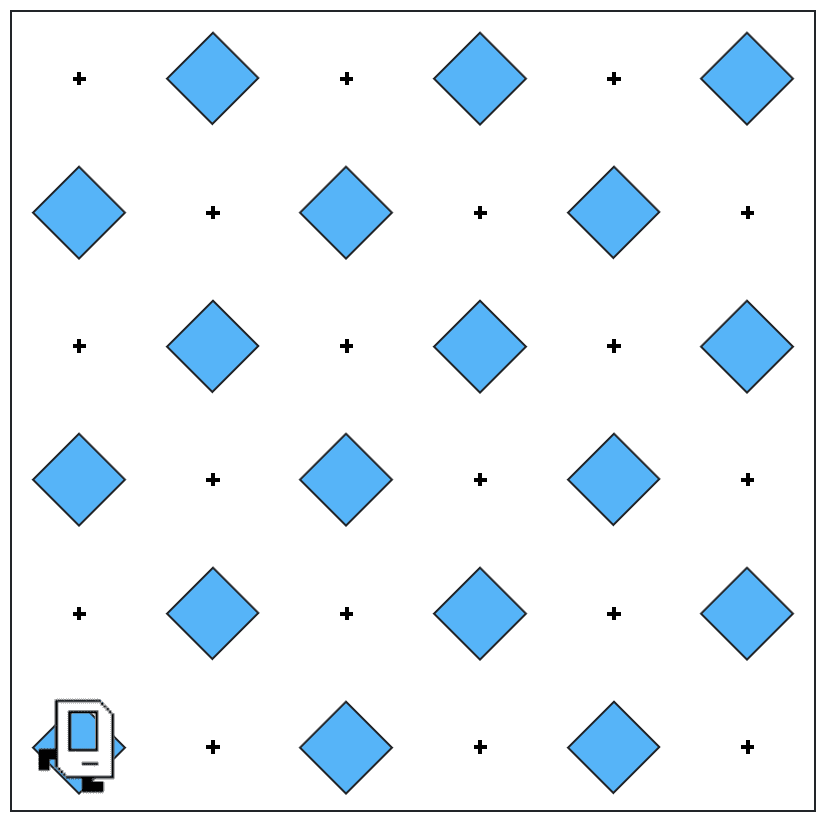
Karel starts and finishes from the same position. We don’t really know how big the world is, or whether there are odd or even numbers of columns or rows, which means that Karel could be working in a world like this:
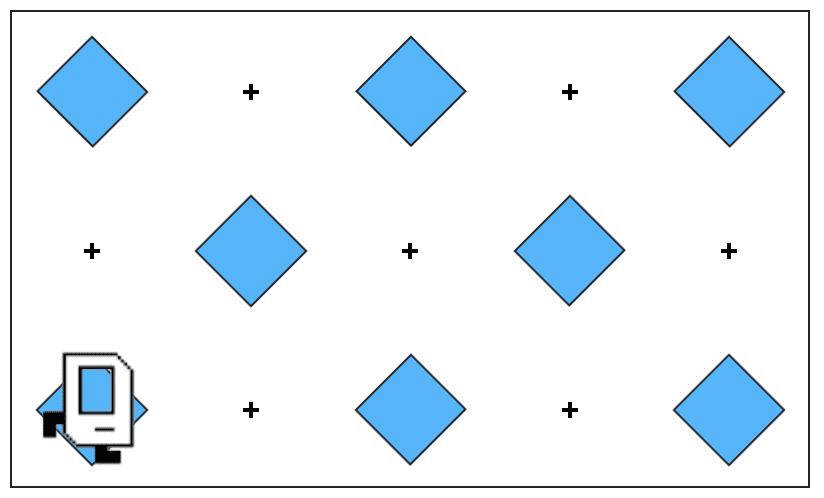
Or this:

The algorithm
Step 1: tag all rows in the first column
One of the most important things to solve here is to let Karel know whether she is on an odd or even row, so that she can correctly lay down the beepers according to the pattern rules. There is no rule on where Karel can go, i.e. east, west, north, south, as long as she doesn’t bang her head against the wall. So my first step is to tag all rows in the first column, like this (we will use the 6×6 world as an example):
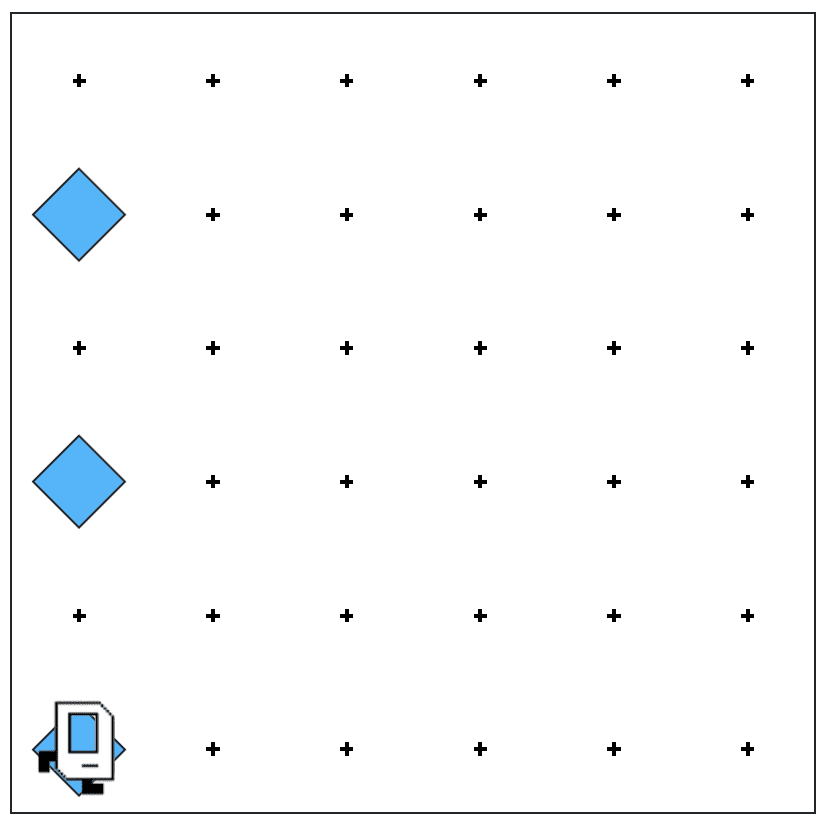
In this way Karel can rely on the “if” function to know whether she is on an odd or even row, therefore know how to proceed.
A remainder: Karel should return to her original corner after tagging all rows.
Step 2: tag one row correctly, regardless of odd or even
This is the core of the solution for Checkerboard Karel.
Since we’ve already tagged all rows, an “if/else” function would do the trick:

If Karel is on an odd row, she simply follows a “move – move – put_beeper” pattern until she stops in front of a wall. If she is on an even row, she follows a “move – put_beeper – move” pattern. Simple as that.
Yet since we don’t know how big or small the world is, Karel needs to check whether her front_is_clear every time she tries to make a move:
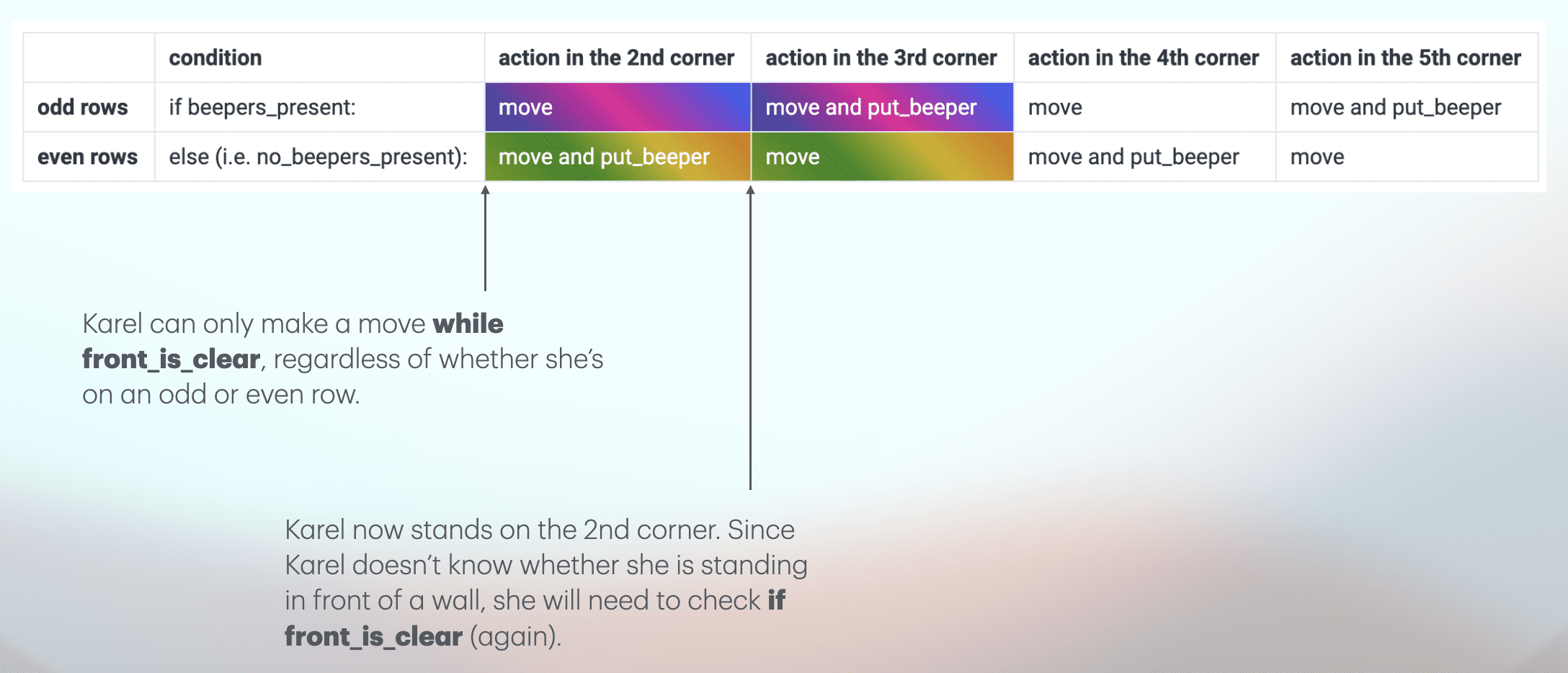
We should also remember to get Karel return to the first corner once she finishes tagging a single row. In this way, Karel will be in the same condition every time, i.e. standing on the first corner, facing east.
Step 3: Karel should tag every row in her world, and return to the original corner afterwards
Because we make Karel return to the first corner on each row after tagging that row, the next step is quite easy:
- Turn left
- Move one step
- Turn right
Then Karel will be on the next row, standing on the first corner, facing east, ready for action.
Except on the last row.
After tagging the last row, Karel must return to the original corner by turning right, moving to the wall, and turning left.
The problem is to find a condition that applies to all rows except the last one, a difference that can help Karel understand when to stop and move to the original corner.
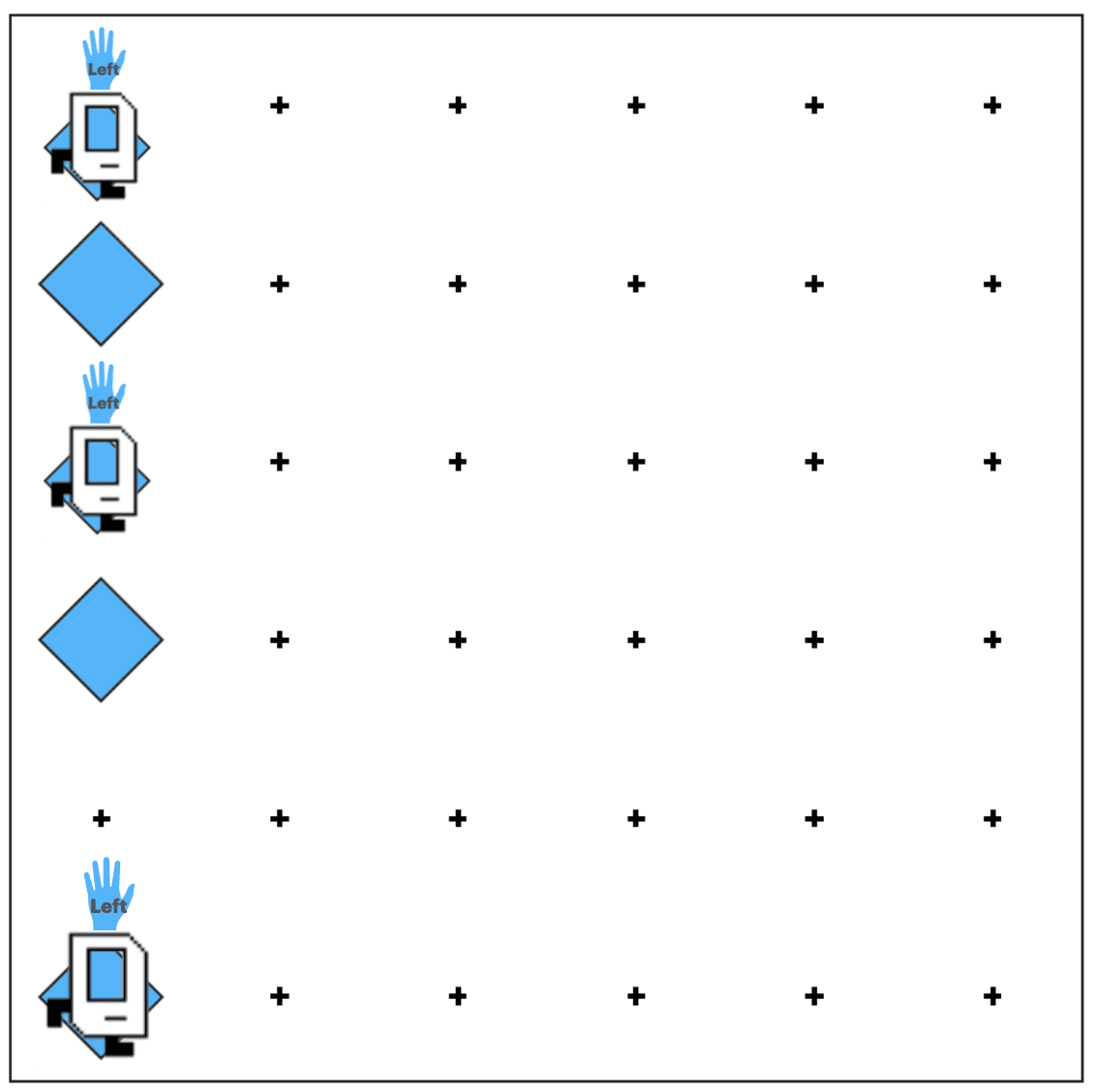
In this world, the power lies with Karel’s left hand.
Imagine Karel can reach out with his left hand and touch if there is a wall. For all rows except the last, Karel’s left_is_clear.
This is the condition we need.
The code
This is my version of the solution, and I’m pretty sure there are other and better ways to solve.
from karel.stanfordkarel import *
"""
Karel should fill the whole world with beepers.
"""
def main():
"""
You should write your code to make Karel do its task in
this function. Make sure to delete the 'pass' line before
starting to write your own code. You should also delete this
comment and replace it with a better, more descriptive one.
"""
tag_all_rows() # this refers to Step 1
tag_row() # this refers to Step 2
while left_is_clear(): #the rest of this section refers to Step 3
turn_left()
move()
turn_right()
tag_row()
turn_right()
move_to_wall()
turn_left()
def tag_all_rows():
turn_left()
put_beeper()
while front_is_clear():
move()
if front_is_clear():
move()
put_beeper()
turn_around()
move_to_wall()
turn_left()
def tag_row():
if beepers_present():
while front_is_clear():
move()
if front_is_clear():
move()
put_beeper()
else:
while front_is_clear():
move()
put_beeper()
if front_is_clear():
move()
turn_around()
move_to_wall()
turn_around()
def turn_around():
turn_left()
turn_left()
def turn_right():
for i in range(3):
turn_left()
def move_to_wall():
while front_is_clear():
move()
# There is no need to edit code beyond this point
if __name__ == '__main__':
main()
Leave a Reply