Fill Karel Solution

Karel needs to fill the entire world with beepers regardless of the size of the world. Other than the first column, the rest of the world are segmented by horizontal walls, preventing Karel from getting to the next row above. Our goal is to write code that does the job no matter how large (or small) the world is.

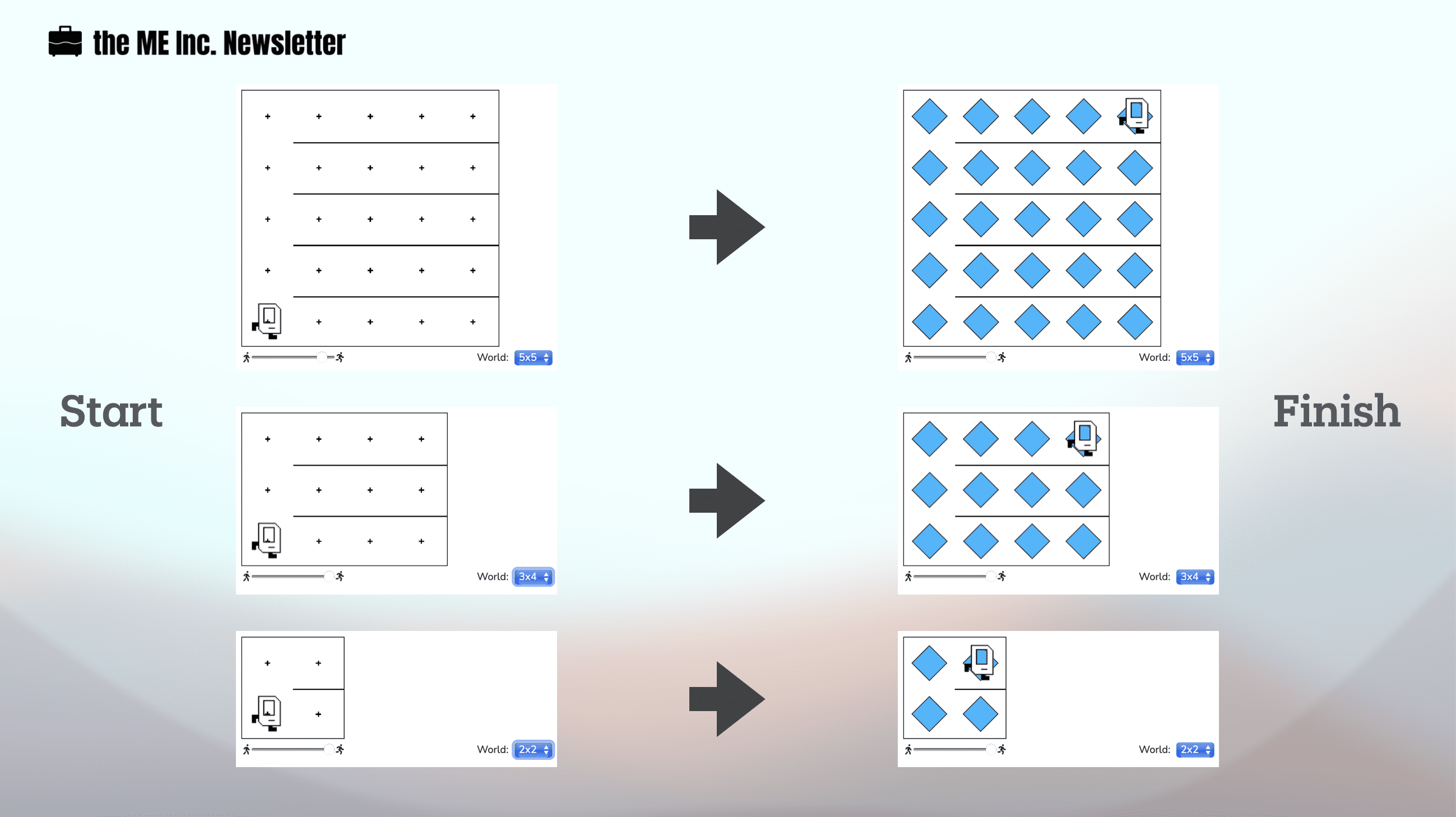
The problem looks pretty daunting at first. How can Karel know when to put beepers or when to move? 

Well the solution lies in decomposition. 

The Thinking Through

If your dad asks you to lay down the tiles in your porch, how would you do that? 

You probably would lay one row of tiles at a time. 

Then you get to the next row and lay down tiles there. So on and so forth.

Until you get to the last row, lay down the tiles, and stop.

That is exactly what we are going to do here:

1. finish one row
2. move to the next row

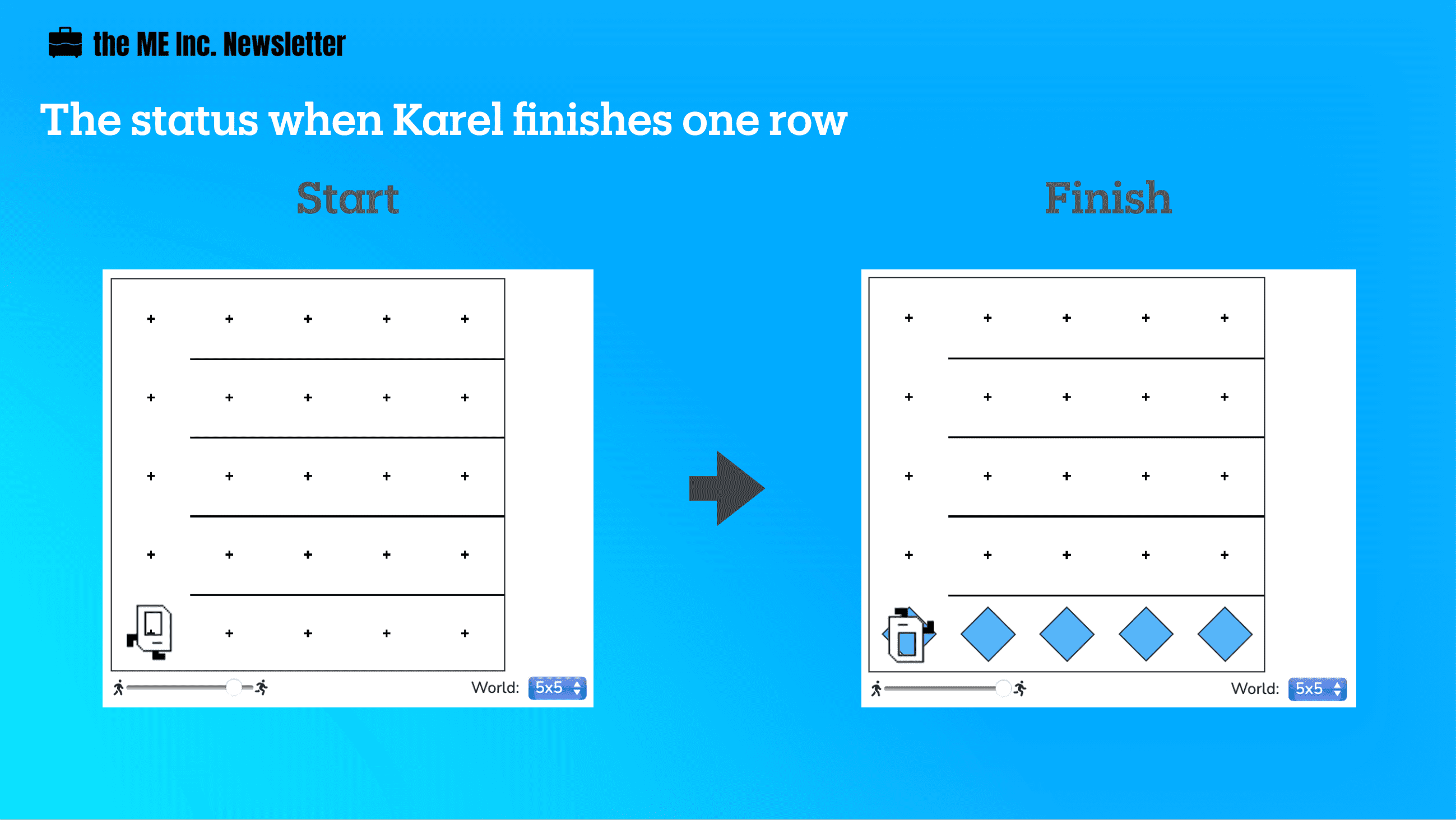
1. Finish One Row

Karel will have only finished a row when she:

1. puts beepers on every spot in that row
2. turns around, and
3. moves all the way back to the wall

At this point, Karel will be facing west, ready to move to the next row.

2. Move to the Next Row

Once Karel finishes a row, she will be ready to move up to the next row. The steps that Karel needs to follow are pretty simple:

1. turn right
2. move
3. turn right

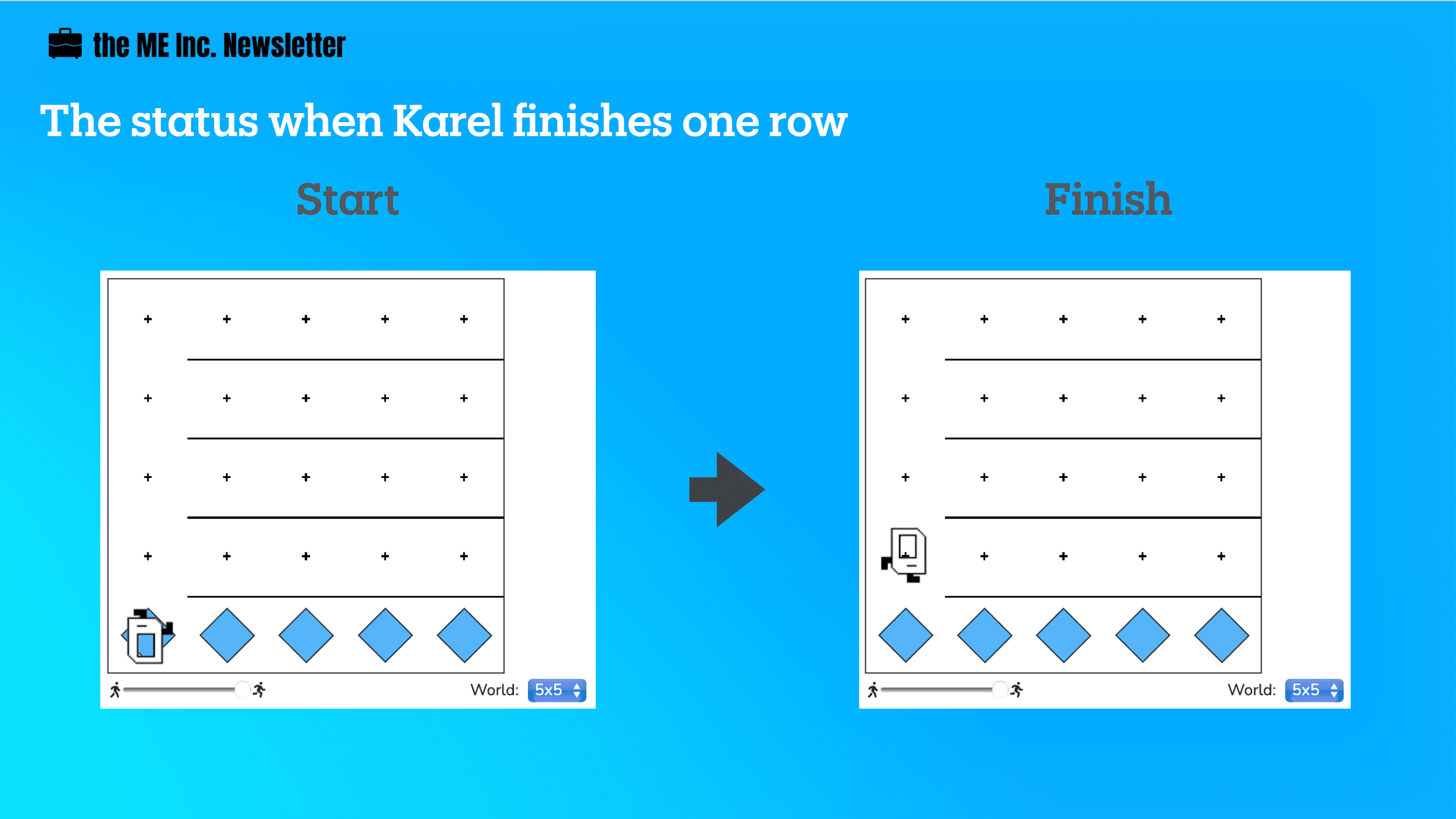
At this point, Karel will be, again, facing an empty row, ready to lay down the beepers for that row, so it's just a matter of repeating the same process.

But when should Karel stop?

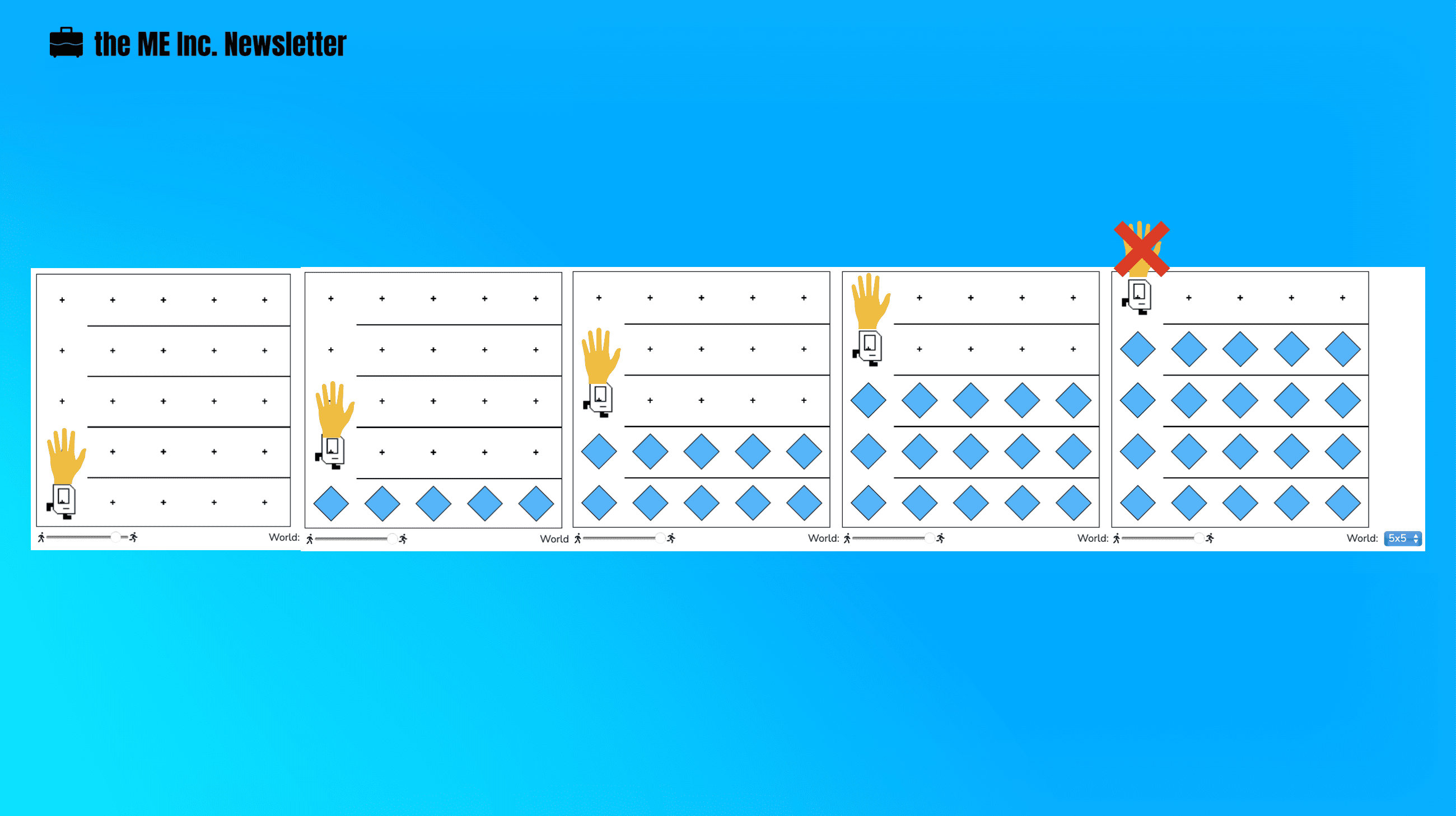
3. The Condition to Stop

For every row other the last one, Karel will return to the first spot after laying down all the beepers, which means Karel "knows" when she is in the last row.

How is it possible that Karel knows this?

Well, we need to find some quality that only the last row has, differentiating it from the rest of rows. 

Every time Karel starts from the first spot, ready to put down beepers for a certain row, her left is clear other than when she is in the last row. It will be easier if you try visualize like Karel is reaching out with her left hand, and only when she is in the last row that her left is NOT clear.

Writing the Code

1. Finish One Row

Recall that to finish one row, Karel will need to do three things:

1. puts beepers on every spot in that row
2. turns around, and
3. moves all the way back to the wall

def finish_one_row():
    laying_tiles()
    turn_around()
    move_to_wall()

We will keep breaking down each of these three functions:

def laying_tiles():
    put_beeper()
    while front_is_clear():
        move()
        put_beeper()

def turn_around():
    turn_left()
    turn_left()

def move_to_wall():
    while front_is_clear():
        move()

2. Move to the Next Row

def move_to_next_row():
    turn_right()
    move()
    turn_right()

def turn_right():
    for i in range(3):
        turn_left()

By this point, we are ready to write the whole thing. Remember that while Karel's left is clear, she should keep finishing one row at a time and move to the next row, and when it's not clear, she should simply lay down the tiles and call it a day.

def main():
    while left_is_clear():
        finish_one_row()
        move_to_next_row()
    laying_tiles()
    
def finish_one_row():
    laying_tiles()
    turn_around()
    move_to_wall()

def turn_around():
    turn_left()
    turn_left()

def move_to_wall():
    while front_is_clear():
        move()

def laying_tiles():
    put_beeper()
    while front_is_clear():
        move()
        put_beeper()
    
def move_to_next_row():
    turn_right()
    move()
    turn_right()

def turn_right():
    for i in range(3):
        turn_left()

# There is no need to edit code beyond this point
if __name__ == '__main__':
    main()

The main function is simple, easy-to-read, and elegant. This is the beauty of decomposition. And by finding the unique quality of the stop condition, we manage to construct a universal solution with the while loop.

0:00

/0:13

1×